Оптимизация
Метод продолжения по параметру
Сущность рассматриваемого варианта метода продолжения по параметру заключается в следующем. Пусть необходимо решить систему нелинейных уравнений
При некотором начальном приближении z
0 вычислим f(z
0)=b. Рассмотрим однопараметрическое семейство нелинейных уравнений
| |
f1(z,τ)=f(z)-(1-τ)b=0 |
(20) |
При t=0, z=z
0 уравнение (20) выполняется автоматически в силу выбора вида функции f
1:
а при τ=1 уравнение (20) совпадает с исходным уравнением (19): f
1(z,1)=f(z). Представим решение задачи (20) в виде функции от параметра продолжения t: z=z(τ). В силу (20), (21) z(τ) определяется системой дифференциальных уравнений
| |
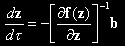 |
(22) |
начальными условиями
Интегрируя систему (22), (23) по τ от 0 до 1, получаем решение исходной задачи (19). Таким образом, решение системы нелинейных уравнений (38) формально сведено к задаче Коши (22), (23). Систему (22) назовем системой дифференциальных уравнений метода продолжения.
При использовании метода Эйлера для интегрирования задачи (20), (21) метод продолжения по параметру становится эквивалентен классическому методу Ньютона. Преимущество этого метода по сравнению с методом Ньютона появляется при использовании более совершенных численных методов интегрирования дифференциальных уравнений. Для идеального метода интегрирования область сходимости рассматриваемого метода продолжения в пространстве параметров z совпадает с областью притяжения искомого решения в этом пространстве. Уравнения (20) имеют особенность на гиперповерхностях с вырожденной матрицей ∂f/∂z, поэтому метод продолжения (как и ньютоновские методы) отказывает при пересечении этих гиперповерхностей. Вырожденность матрицы ∂f/∂z обычно имеет место на границе области притяжения решения и связана с ветвлением решений исходной системы (19).
Правые части системы уравнений (15) или (15а) численно осреднялись по схеме (16) в процессе интегрирования этой системы. Для осреднения использовались простые численные методы интегрирования функций (метод трапеций или метод Симпсона) на фиксированной равномерной сетке по F из 30-300 узлов на витке. Интегрирование осредненной системы (15) проводилось с помощью явного метода Рунге-Кутта 7 (8) порядка (метод Дормана-Принса) с начальными условиями
| |
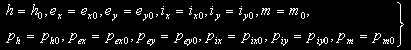 |
(23) |
при t = 0. Для задачи оптимального быстродействия начальное значение массы является параметром. Условия на массу и сопряженную к ней переменную в этом случае должны быть исключены из (24).
Метод продолжения по параметру показал свою высокую эффективность при решении задачи оптимального быстродействия. Для большинства задач сходимость к оптимальному решению обеспечивалась выбором следующего начального приближения для вектора параметров краевой задачи:
| |
ph = 1, pex = pey = pix = piy = 0, T = 1 |
где T - безразмерное время, отнесенное к начальной орбите КА. При вариации параметров начальной и конечной орбит в качестве начального приближения использовались начальные значения сопряженных переменных и времени перелета, полученные при решении предыдущей задачи.
К сожалению, для задачи с фиксированным временем перелета метод продолжения оказался недостаточно эффективным в связи с разрывностью правых частей дифференциальных уравнений (22) при появлении или исчезновении участков траектории в процессе продолжения. В этом случае для решения краевой задачи использовался модифицированный метод Ньютона, а в качестве начального приближения использовались начальные значения сопряженных переменных, полученные в результате решения задачи оптимального быстродействия.
СПИСОК ЛИТЕРАТУРЫ
| 1 |
Sackett L.L., Malchow H.L., Edelbaum T.N. Solar Electric Geocentric Transfer with Attitude Constraints: Analysis. NASA CR-134927, 1975. |
| 2 |
Geffroy S. Generalisation des Techniques de Moyennation en Controle Optimal - Application aux Problemes de Transfert et Rendez-Vous Orbitaux a Poussee Faible, November 1997. |
| 3 |
Cano J.L., Schoenmaekers J., Jehn R., et al. SMART-1 Mission Analysis: Collection of Notes on the Moon Mission. S1-ESC-RP-5004, 1999. |
| 4 |
Olesen S.R., Myers R.M., Kluever C.A., et al. Advance Propulsion for Geostationary Orbit Insertion and North-South Station Keeping // J. Spacecraft and Rockets. 1997. V. 34, No. 1. |
| 5 |
Schwer A.G., Schottle U.M., Messerschmid E. Operational Impacts and Environmental Effects on Low-Thrust Transfer-Missions of Telecommunication Satellites // 46th International Astronautical Congress. IAF-95-S.3.10. Norway, Oslo, 1995. |
| 6 |
Spitzer A. Novel Orbit Raising Strategy Makes Low Thrust Commercially Viable // 24th International Electric Propulsion Conference, IEPC 95-212, Russia, Moscow, 1995. |
| 7 |
Medvedev A., Khatulev V., Yuriev V., et al. Combined flight profile to insert telecommunication satellite into geostationary orbit using "Rockot" light-weight class launch vehicle // 51st International Astronautical Congress. IAF-00-V.2.09, Brasilia, Rio de Janeiro, 2000. |
| 8 |
Konstantinov M.S., Fedotov G.G., Petukhov V.G., et al. Electric Propulsion Mission to GEO Using Soyuz/Fregat Launch Vehicle. // 52nd International Astronautical Congress. IAF-01-V.3.02, France, Toulouse, 2001. |
| 9 |
Medvedev A., Khatulev V., Yuriev V., et al. Lunar and Planetary Missions Using Rockot Launch Vehicle. IAA-L-0704P. |
| 10 |
Petukhov V. One Numerical Method to Calculate Optimal Power-Limited Trajectories // International Electric Propulsion Conference. IEPC-95-221, Russia, Moscow, 1995. |
| 11 |
Eneev T.M., Konstantinov M.S., Egorov V.A., et al. Some Methodical Problems of Low-Thrust Trajectory Optimization. Preprint of KIAM No. 110, Moscow, 1996. |
| 12 |
Eneev T.M., Konstantinov M.S., Akhmetshin R.Z., et al. Mercury-to-Pluto Range Missions Using Solar-Nuclear Electric Propulsion. Preprint of KIAM No. 111, Moscow, 1996. |
| 13 |
Hairer F., Norsett S.P., Wanner G. Solving Ordinary Differential Equations I. Non-Stiff Problems. Spinger-Verlag, Berlin, 1987. |
| 14 |
Лебедев В.Н. Расчет движения космического аппарата с малой тягой. М., Изд.-во ВЦ АН СССР, 1968. |