Оптимизация

---

ОПТИМИЗАЦИЯ МНОГОВИТКОВЫХ ПЕРЕЛЕТОВ МЕЖДУ НЕКОМПЛАНАРНЫМИ ЭЛЛИПТИЧЕСКИМИ ОРБИТАМИ

Рассматривается задача оптимизации межорбитальных перелетов космического аппарата (КА) с двигательной установкой малой тяги между некомпланарными эллиптическими орбитами в центральном гравитационном поле. Задача оптимизации траектории межорбитального перелета сводится к решению краевой задачи для системы обыкновенных дифференциальных уравнений с помощью формализма принципа максимума.

Уравнения движения

Рассмотрим движение КА под действием двух сил: гравитационной силы притягивающего центра и силы тяги ЭРДУ. Величины тяги и скорости истечения включенной ЭРДУ считаются постоянными, на ориентацию вектора тяги не накладывается каких-либо ограничений. Гравитационное поле притягивающего центра будем считать центральным ньютоновским. Запишем компоненты реактивного ускорения в орбитальной системе координат:

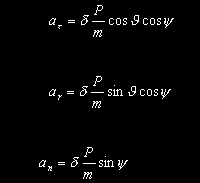(1)

aτ, ar, an - соответственно трансверсальная, радиальная и бинормальная проекции реактивного ускорения, δ - функция включения двигателя (δ =1 при включенной ЭРДУ и δ =0 при неработающей ЭРДУ), P - величина реактивной тяги, m - масса КА, Ψ - угол рысканья, Θ - угол тангажа

Для исключения особенностей в окрестности нулевых значений эксцентриситета и наклонения, перейдем от классических кеплеровсих элементов к равноденственным элементам:

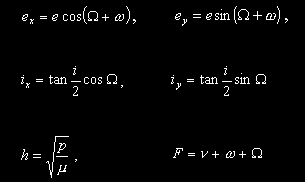p - фокальный параметр, e - эксцентриситет, ω - аргумент перицентра, i - наклонение, Ω - долгота восходящего узла, υ - истинная аномалия, µ - гравитационный параметр центрального тела

Уравнения орбитального движения КА в равноденственных элементах примут следующий вид:

(2)

где:

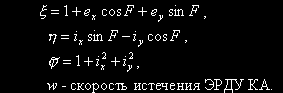
Оптимальное управление

Запишем краевые условия.

Требуется перевести КА начальной массы m0 с начальной орбиты

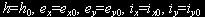(3)
на конечную

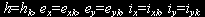(4)
за время T.

Рассматривается задача минимизации функционала соответствующая задаче о перелете с минимальными затратами топлива. Отметим, что при отсутствии ограничений на время перелета T и при d є 1, функционал (5) соответствует задаче о перелете за минимальное время. Более традиционным, однако, для задачи оптимального быстродействия является функционал

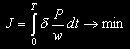(5)

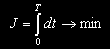(5a)

В задаче межорбитального перелета за минимальное время разница между функционалами (5) и (5а) через условие трансверсальности сводится к различной нормировке вектора сопряженных переменных.

Для решения задачи (2-5) используем формализм принципа максимума. Гамильтониан задачи оптимального управления (2-5) имеет вид

(6)

где

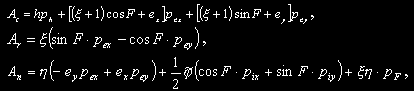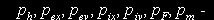переменные, сопряженные к фазовым координатам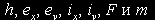

Оптимальное управление δ(t), J(t), ψ(t) определяется из условия максимума гамильтониана (6):

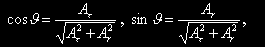	(7)
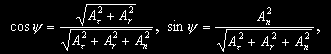	(8)
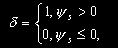	(9)

где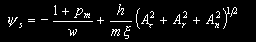

- функция переключения.

В задаче о перелете за минимальное время вместо соотношения (9) используется тождество

δє1,

(10)

а дифференциальные уравнения для переменных m и pm можно исключить из рассмотрения, используя явную зависимость массы КА m от времени:

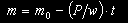(11)

вперед >>

1 2 3